问题
单项选择题
设A，B为n阶矩阵，考虑以下命题：
①若A，B为等价矩阵，则A，B的行向量组等价．
②若行列式|A|=|B|，则A，B为等价矩阵．
③若Ax=0与Bx=0都只有零解，则A，B为等价矩阵．
④若A，B为相似矩阵，则Ax=0与Bx=0的解空间的维数相同．
以上命题中正确的是
A．①③．
B．②④．
C．②③．
D．③④．
答案
参考答案：D
解析：[详解] A，B等价推不出A，B的行向量组等价．
如：
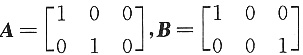，A，B等价，但A，B行向量组并不等价．可排除(A)．
若|A|=|B|，但r(A)未必与r(B)相等．可排除(B)，(C)．
故选(D)．