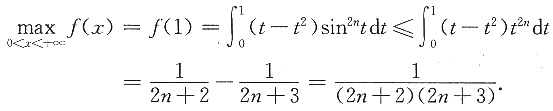问题
问答题
设
，其中x≥0，n为正整数，试证明：
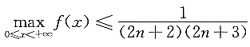
答案
参考答案：
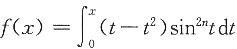，f’(x)=(x-x2)sin2nx，x＞0．
令f’(x)=0，得x0=1，xk=kπ(k=1，2，…)．
因为当x＞1时，x-x2＜0，sin2nx＞0(x≠kπ)，在xk的左右两侧，f’(x)＜0，因此，xk不是f(x)的极值点．
又因当0＜x＜1时，f’(x)＞0，当1＜x＜π时，f’(x)＜0，故f(1)是极大值．
由极值的唯一性，可知
