问题
问答题
设A为三阶矩阵，λ1，λ2，λ3是A的三个不同的特征值，对应的特征向量为α1，α2，α3，令β=α1+α2+α3．
证明：β，Aβ，A2β线性无关．
答案
参考答案：设k1β+k2Aβ+k3A2β=0， ①
由题设Aαi=αi(i=1，2，3)，于是
将②，③代入①式，整理得
因为α1，α2，α3为三个不同的特征值所对应的特征向量，所以线性无关，于是有
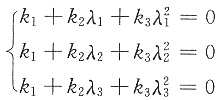，其系数行列式
，所以k1=k2=k3=0，故β，Aβ，A2β线性无关
