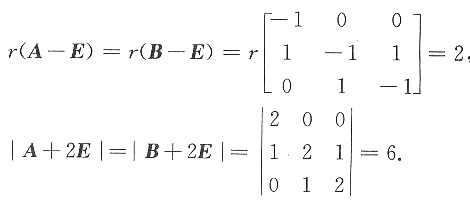问题
问答题
设A为三阶矩阵，λ1，λ2，λ3是A的三个不同的特征值，对应的特征向量为α1，α2，α3，令β=α1+α2+α3．
若A3β=Aβ，求秩r(A-E)及行列式|A+2E|．
答案
参考答案：由A3β=Aβ，有
，
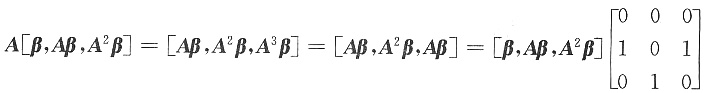令P=[β，Aβ，A2β]，则P=[β，Aβ，A2β]可逆，且
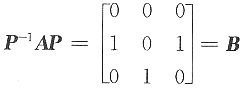
从而有
搜题请搜索小程序“爱下问搜题”
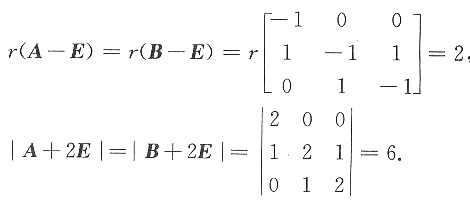
设A为三阶矩阵，λ1，λ2，λ3是A的三个不同的特征值，对应的特征向量为α1，α2，α3，令β=α1+α2+α3．
若A3β=Aβ，求秩r(A-E)及行列式|A+2E|．
参考答案：由A3β=Aβ，有
，
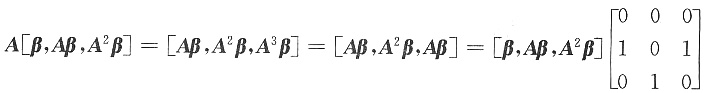令P=[β，Aβ，A2β]，则P=[β，Aβ，A2β]可逆，且
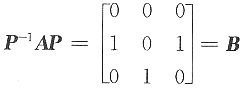
从而有