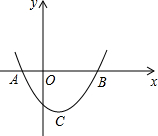
在一个不透明的盒子里装有5个分别写有数字-2,-1,0,1,2的小球,它们除数字不同外其余全部相同.现从盒子里随机取出一个小球,将该小球上的数字作为点P的横坐标,将该数的立方作为点P的纵坐标,则点P落在抛物线y=x2-3x-5与x轴所围成的区域内(含边界)的概率是______.
如图:
∵-2,-1,0,1,2的立方为-8,-1,0,1,8.
∴点P的坐标为(-2,-8),(-1,-1),(0,0),(1,1),(2,8);
∴抛物线y=x2-3x-5与x轴交点为(
,0),(3+ 29 2
,0),抛物线y=x2-3x-5的顶点坐标为(3- 29 2
,-3 2
),29 4
∵-2<
,3- 29 2
∴(-2,-8)不在抛物线y=x2-3x-5与x轴所围成的区域内,
(-1,-1)是抛物线y=x2-3x-5上的点,在边界上,
(0,0)在x轴上,即在边界上,
(1,1),(2,8)在第一象限,也不在抛物线y=x2-3x-5与x轴所围成的区域内;
∴点P落在抛物线y=x2-3x-5与x轴所围成的区域内(含边界)的有(0,0),(-1,-1),
∴点P落在抛物线y=x2-3x-5与x轴所围成的区域内(含边界)的概率是:
.2 5
故答案为:
.2 5