在一个不透明的口袋里有分别标注2、4、6的3个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢.
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.
小红要想在游戏中获胜,她会选择哪一种规则,并说明理由.
(1)列表如下:

画树状图如下:
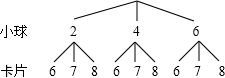
共有9种可能,分别是(2,6),(2,7),(2,8),(4,6),(4,7),(4,8),(6,6),(6,7),(6,8);
(2)从图表或树状图可知,至少有一次是“6”的情况有5种,
所以,小红赢的概率是P(至少有一次是“6”)=
,5 9
小莉赢的概率是
,4 9
∵
>5 9
,4 9
∴此规则小红获胜的概率大,
卡片上的数字是球上数字的整数倍的有:(2,6)(2,8)(4,8)(6,6)共4种情况,
所以,小红赢的概率是P(卡片上的数字是球上数字的整数倍)=
,4 9
小莉赢的概率是
,5 9
∵
>5 9
,4 9
∴此规则小莉获胜的概率大,
∴小红要想在游戏中获胜,她应该选择规则1.
