问题
选择题
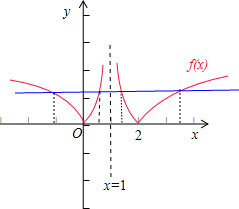
已知函数f(x)=|loga|x-1||(a>0,a≠1),若x1<x2<x3<x4,且f(x1)=f(x2)=f(x3)=f(x4),则
|
答案
设g(x)=|loga|x||,则g(x)为偶函数,
图象关于y轴对称,
而函数f(x)=|loga|x-1||是把g(x)的图象向右平移
一个单位得到的,
故g(x)的图象关于直线x=1对称.
∵x1<x2<x3<x4,
且f(x1)=f(x2)=f(x3)=f(x4),
∴x1+x4=1,x2+x3=1.
再由函数f(x)的图象特征可得,logax1=-logax2,
logax3=-logax4,
∴x1x2=x3x4=1,
∴
+1 x1
+1 x2
+1 x3 1 x4
=
+x1+x2 x1x2 x3+x4 x3x4
=1+1
=2.
故选:A.