问题
实验题
某同学在“用打点计时器测速度”的实验中，用打点计时器记录了被小车拖动的纸带的运动情况，在纸带上确定出A、B、C、D、E、F、G共7个计数点，其相邻点间的距离如图所示.每两个相邻的计数点之间的时间间隔为0.10s.
完成下列填空和作图：
(1)每两个计数点间还有 个点没有标出.
(2)试根据纸带上各个计数点间的距离，每隔0.10s测一次速度，计算出打下B、C、D、E、F五个点时小车的瞬时速度，并将各个速度值填入下表(保留3位有效数字)
| vB | vC | vD | vE | vF | |
| 数值（m/s） |
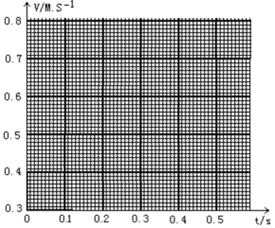
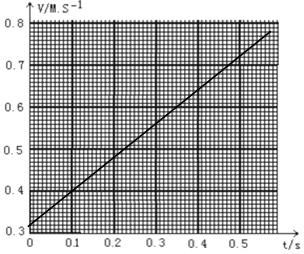
(4) 将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中，并画出小车的瞬时速度随时间变化的关系图线.
答案
（10分）
（1）4
（2）0.400 0.479 0.560 0.640 0.721
（3）0.8
（4）略
（1）每两个相邻计数点之间还有四个点未画出，所以相邻的计数点间的时间间隔T=0.1s．
（2）根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，vB=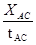
="0.400" m/s，同理：vC="0.479" m/s，vD="0.560" m/s， vE="0.640" m/s，vF="0.721" m/s，
（3）根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，得：x4-x1=3a1T2 x5-x2=3a2T2 x6-x3=3a3T2
为了更加准确的求解加速度，我们对三个加速度取平均值得：a=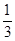
（a1+a2+a3）即小车运动的加速度计算表达式为：
a=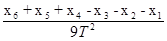
即：a=0.801m/s2
（4）将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中，画出小车的瞬时速度随时间变化的关系图线．
要学会应用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用