问题
填空题
已知一个口袋中装有四个完全相同的小球,小球上分别标有-1,0,1,2四个数,搅匀后一次从中摸出两个小球,将小球上的数分别用a,b表示,将a、b代入方程组
|
答案
∵一次从中摸出两个小球,相当于摸一次,不放回再摸一次小球,画出树状图得:
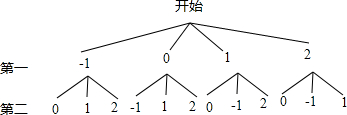
∴a,b的不同组合为:(-1,0),(-1,1),(-1,2),(0,-1),(0,1),(0.2),(1,0),(1,-1),(1,2),(2,0)(2,-1),(2,1),或(0,-1),(1,-1)(2,-1),(-1,0),(1,0),(2,0),(0,1),(-1,1),(2,1),(0,2),(-1,2),(1,2);
解方程组
得:ax-y=1 x+by=b
,x= 2b ab+1 y= ab-1 ab+1
若方程组有解则:ab≠-1,即可,
∴(-1,1),(1,-1),(1,-1),(-1,1)不满足题意,
∴将a、b代入方程组
,则方程组有解的概率是:P=ax-y=1 x+by=b
=20 24
,5 6
故答案为:
.5 6
