如图，过点Q作QG∥AB交OD于点G，过点F作FH∥AB交OA于H，

则△DGQ是等腰直角三角形，

∴DQ=QG，

又∵BP=DQ，

∴BP=QG，

由QG∥AB得，∠P=∠FQG，

在△PBF和△QGF中，

∠P=∠FQG ∠PFB=∠QFG BP=QG

，

∴△PBF≌△QGF（AAS），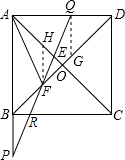

∴PF=QF，

∴PQ=2AF=2

5

，

设BP=DQ=x，

则AB=3+x，AQ=3-x，

在Rt△APQ中，PQ²=AP²+AQ²，

即（2

5

）²=（3+x）²+（3-x）²，

解得x=1，

在Rt△AOF中，AO=BO=

3 2

2

，

OF=

AF2-AO2

=

5 2-( 3 2 2 )2

=

2

2

，

由FH∥AB得，

HF

AB

=

OF

BO

，

即

HF

3

=

2 2

3 2 2

，

解得HF=1，

HF

AP

=

EF

PE

，

即

1

3+1

=

EF

5 +EF

，

解得EF=

5

3

．

故答案为：

5

3

．