问题
计算题
如图所示，轨道由斜面和水平两部分组成，斜面轨道倾角为θ=60°，斜面的水平投影长为L0=5m，水平轨道足够长，一小球从斜面顶端静止释放，释放的同时开始计时，在斜面上加速下滑的加速度为a1=5m/s2，在水平上减速运动的加速度为a2=2m/s2，不计小球在轨道连接处的碰撞和速率变化，求：
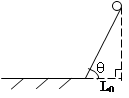
（1）小球从释放到斜面中点的时间；
（2）小球运动到轨道连接处的速率；
（3）小球运动6s经过的位移。
答案
（1）t=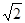
s（2）v=10m/s（3）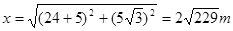
题目分析：（1）斜面长度为L，根据cosθ= L0/L, L=10m 1分
根据L/2=at2/2 2分
t=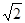s 1分
(2)根据v2=2aL 2分
v=10m/s 1分
(3)小球在斜面上下滑的时间t1=v/a1=2s
小球在水平上向左减速的时间t2=v/a2=5s
因此小球在第6s末速度不为零
前2s在斜面上运动的水平和竖直位移分别为5m和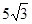
m 1分
后4s在水平上运动的位移为L’，
根据L’=vt-at2/2 =10×(6-2)-2×(6-2)2/2=24m 1分
所以6s内的位移为x，
根据勾股定理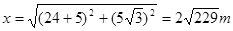， 1分
点评：基础题，关键对是公式的正确掌握以及利用