问题
解答题
已知函数f(x)=loga(ax-1)(a>0且a≠1),
(1)求f(x)的定义域;
(2)讨论f(x)的单调性;
(3)x为何值时,函数值大于1。
答案
解:(1)f(x)=loga(ax-1)有意义,应满足ax-1>0,即ax>1,
当a>1时,x>0;
当0<a<1时,x<0;
因此,当a>1时,函数f(x)的定义域为{x|x>0};
当0<a<1时,函数f(x)的定义域为{x|x<0}.
(2)当a>1时,y=ax-1为增函数,因此y=loga(ax-1)为增函数;
当0<a<1时,y=ax-1为减函数,因此y=loga(ax-1)为增函数;
综上所述,y=loga(ax-1)为增函数;
(3)当a>1时,f(x)>1,即ax-1>a,
∴ax>a+1,∴x>loga(a+1);
当0<a<1时,f(x)>1,即0<ax-1<a,
∴1<ax<a+1,∴loga(a+1)<x<0。

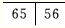 缺失,要求可摘局部义齿修复。检查见余留牙情况良好,下颌舌侧牙槽骨呈斜坡状。拟
缺失,要求可摘局部义齿修复。检查见余留牙情况良好,下颌舌侧牙槽骨呈斜坡状。拟 为基牙,采用弯制连接杆连接。活动义齿修复。
为基牙,采用弯制连接杆连接。活动义齿修复。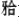 ,咬合紧
,咬合紧