问题
解答题
已知函数f(x)=log2(|x-l|+|x-5|-a).
(Ⅰ)当a=2时,求函数f(x)的最小值;
(Ⅱ)当函数f(x)的定义域为R时,求实数a的取值范围。
答案
解:函数的定义域满足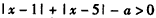 ,
,
即 ,
,
(Ⅰ)当a=2时, ,
,
设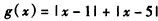 ,则
,则
 ,
,
g(x)min=4·f(x)min=log2(4-2)=1。
(Ⅱ)由(Ⅰ)知,g(x)=|x-l|+|x-5|的最小值为4,
|x-l|+|x-5|-a>0,
∴a<4,
∴a的取值范围是(-∞,4)。
