解：（1）∵f（x）=log₄（ax²+2x+3）且f（1）=1，

∴log₄（a●1²+2×1+3）=1a+5=4a=﹣1

可得函数f（x）=log₄（﹣x²+2x+3）

∵真数为﹣x²+2x+3＞0﹣1＜x＜3

∴函数定义域为（﹣1，3）

令t=﹣x²+2x+3=﹣（x﹣1）²+4 可得：

当x∈（﹣1，1）时，t为关于x的增函数；

当x∈（1，3）时，t为关于x的减函数．

∵底数为4＞1

∴函数f（x）=log₄（﹣x²+2x+3）的单调增区间为（﹣1，1），单调减区间为（1，3）

（2）设存在实数a，使f（x）的最小值为0，由于底数为4＞1，

可得真数t=ax²+2x+3≥1恒成立，且真数t的最小值恰好是1，

即a为正数，且当x=﹣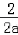=﹣时，t值为1．

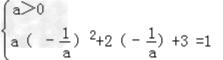
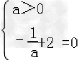
所以a=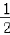

所以a=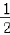，使f（x）的最小值为0．