问题
解答题
已知函数f(x)=lg(1+x)-lg(1-x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性。
答案
解:(1)由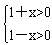 ,得-1<x<1,
,得-1<x<1,
∴函数f(x)的定义域为(-1,1);
(2)定义域关于原点对称,对于任意的x∈(-1,1),有-x∈(-1,1),
f(-x)=lg(1-x)-lg(1+x)=-f(x),
∴f(x)为奇函数.
已知函数f(x)=lg(1+x)-lg(1-x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性。
解:(1)由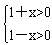 ,得-1<x<1,
,得-1<x<1,
∴函数f(x)的定义域为(-1,1);
(2)定义域关于原点对称,对于任意的x∈(-1,1),有-x∈(-1,1),
f(-x)=lg(1-x)-lg(1+x)=-f(x),
∴f(x)为奇函数.