问题
解答题
已知函数f(x)=ln(ax-bx)(a>1>b>0)。
(1)求函数f(x)的定义域I;
(2)判断函数f(x)在定义域I上的单调性,并说明理由;
(3)当a,b满足什么关系时,f(x)在[1,+ ∞)上恒取正值。
答案
解:(1)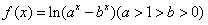 有意义,需满足
有意义,需满足 ,
,
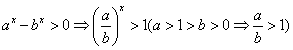 ,
,
∴函数的定义域为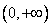 。
。
(2)函数在定义域上是单调递增函数;
证明: ,
,
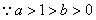 ,
,
∴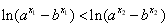 ,
,
∴ ,
,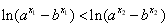 ,
,
∴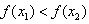 ,
,
所以,原函数在定义域上是单调递增函数。
(3)要使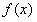 在
在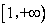 上恒取正值,须
上恒取正值,须 在
在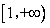 上的最小值大于0,
上的最小值大于0,
由(2)知,ymin=f(1)=ln(a-b),
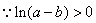 ,
,
∴a-b>1,
所以,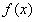 在
在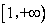 上恒取正值时有a-b>1。
上恒取正值时有a-b>1。
