问题
解答题
设函数f(x)=loga（ax-1）（a＞0且a≠1）。
（1）求f(x)的定义域；
（2）当a＞1时，求使f(x)＞0的x的范围。
答案
解：（1）f(x)函数的定义域由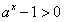
，
当a＞1时，ax-1＞0，解得：x＞0；
当0＜a＜1时，ax-1＞0，解得：x＜0。
（2）当a＞1时，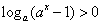
，即
，
∴
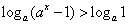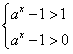，解得：x＞loga2，
∴x的取值范围是
。
搜题请搜索小程序“爱下问搜题”
设函数f(x)=loga（ax-1）（a＞0且a≠1）。
（1）求f(x)的定义域；
（2）当a＞1时，求使f(x)＞0的x的范围。
解：（1）f(x)函数的定义域由，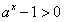
当a＞1时，ax-1＞0，解得：x＞0；
当0＜a＜1时，ax-1＞0，解得：x＜0。
（2）当a＞1时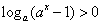，，即，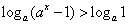
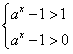∴，解得：x＞loga2，
∴x的取值范围是。