问题
解答题
函数f（x）=loga(3-ax）（a>0，a≠1）
（1）当a=2时，求函数f（x）的定义域；
（2）是否存在实数a，使函数f（x）在[1，2]递减，并且最大值为1，若存在，求出a的值；若不存在，请说明理由。
答案
解：由题意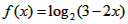
，∴3-2x＞0，即x＜
，
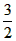所以函数f（x）的定义域为（-∞，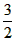
）；
（2）令u=3-ax，则u=3-ax在[1，2]上恒正，∵a>0，a≠1，∴u=3-ax在[1，2]上单调递减，
∴3-a·2＞0，即a∈（0，1）∪（1，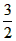
）
又函数f（x）在[1，2]递减，∵u=3-ax在[1，2]上单调递减，∴a>1，即a∈（1，）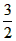
又∵函数f（x）在[1，2]的最大值为1，∴f（1）=1
即f（x）=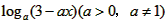
∴a=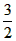
∵a=
与a∈（1，）矛盾，∴a不存在。