问题
解答题
已知函数f(x)=lg(ax-bx)，a＞1＞b＞0，
（1）求f(x)的定义域；
（2）在函数f(x)的图象上是否存在不同的两点，使过这两点的直线平行于x轴；
（3）当a，b满足什么条件时，f(x)在(1，+∞)上恒取正值。
答案
解：(1)由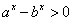
得
，
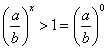由于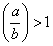
，所以x＞0，
即f(x)的定义域为（0，+∞）。
(2)任取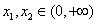
，且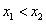
，
，
，
，
∴
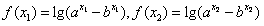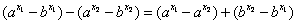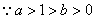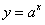在R上为增函数，
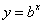在R上为减函数，
∴
，
∴
，
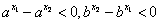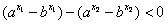即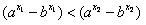
，
又∵y=lgx在（0，+∞）上为增函数，
∴
，
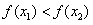∴f(x)在（0，+∞）上为增函数，
所以任取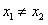
，则必有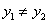
，
故函函数f(x)的图象L不存在不同的两点使过两点的直线平行于x轴。
(3)因为f(x)是增函数，所以当x∈（1，+∞）时，f(x)＞f(1)，
这样只需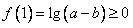
，
即当a-b≥1时，f(x)在（1，+∞）上恒取正值。