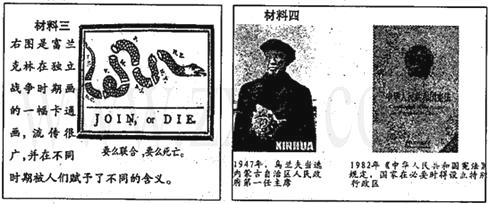
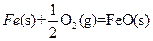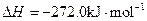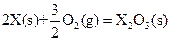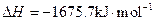数列{an}满足a1>1,an+1-1=an(an-1),(n∈N+),且
|
a1>1,由an+1-1=an(an-1),(n∈N+)知,对所有n,an>1,
等式两边取倒数,得
=1 an+1-1
=1 an(an-1)
-1 an-1
,得,1 an
=1 an
-1 an-1
,1 an+1-1
则
+1 a1
+…+1 a2
=1 a2012
-1 a1
=21 a2013
整理可得,a2013=
,2-a1 3-2a1
a2013-4a1=2(3-2a1)+
-1 2(3-2a1)
≥211 2
-(3-2a1) 1 3-2a1
=-11 2
.7 2
则a2013-4a1的最小值为 -
.7 2
故答案为:-
.7 2

 素,其原子序数依次增大。W、Y的氧化物是导致酸雨的主要物质,X的基态原子核外有7个原子轨道填充了电子,Z能形成红色(或砖红色)的
素,其原子序数依次增大。W、Y的氧化物是导致酸雨的主要物质,X的基态原子核外有7个原子轨道填充了电子,Z能形成红色(或砖红色)的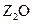 和黑色的ZO两种氧化物。
和黑色的ZO两种氧化物。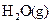 __________(填“强”或“弱”)。
__________(填“强”或“弱”)。