问题
解答题
已知数列{an}满足：a1=1，a2=a（a＞0），数列{bn}满足bn=anan+1（n∈N*）。
（Ⅰ）若{an}是等差数列，且b3=12，求数列{an}的通项公式；
（Ⅱ）若{an}是等比数列，求数列{bn}的前n项和Sn；
（Ⅲ）若{bn}是公比为a-1的等比数列时，{an}能否为等比数列？若能，求出a的值；若不能，请说明理由。
答案
解：（Ⅰ）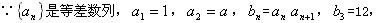
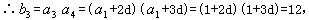
即d=1或d=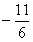
，
又因a=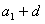
=1+d＞0， 得d＞-1，
∴d=1，∴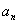
=n。
（Ⅱ）
，
∴
。
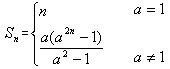（Ⅲ）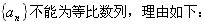
∴
，
∴
，
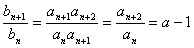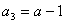假设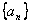
为等比数列，
，
因此此方程无解，所以数列一定不能等比数列。