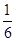
设S△BCE=x，S△AEF=y，因AD‖BC，AE:EB="1" :2。

所以△ADE∽△BCE，EB/AE=CE/ED=2/1

S△ADE/S△BCE=(AE/EB)²=1/4，S△ADE=x/4

又因为EF‖BC,

所以EF∥AD，△CEF∽△CDA，S△CEF/S△CDA=（CE/CD)²=4/9

S△CEF/S四边形ADEF=4/5，S△CEF=4/5（y+x/4）

因△AEF∽△ACB，

所以S△AEF/S△ACB=（AE/AB)²=1/9，

S△AEF/S四边形BEFC=1/8

即：y/（4/5（y+x/4）+x）=1/8

解得 y/x=1/6

S△AEF:S△BCE=1：6