问题
解答题
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本，得频率分布表如下：
（2）为了选拔出更优秀的学生，高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核，分别求第三、四、五各组参加考核人数； （3）在（2）的前提下，高校决定在这6名学生中录取2名学生，求2人中至少有1名是第四组的概率． | ||||||||||||||||||||||||||||
答案
（1）①的位置为12， ②的位置为0.30（2）3，2，1（3）0.6
题目分析：解：（1）①的位置为12， ②的位置为0.30
（2）抽样比为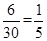
，所以第三、四、五组抽中的人数为
、
、
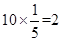（3）设2人中至少有1名是第四组为事件A，则P(A)＝１－0.4＝0.6（4分）
点评：解决的关键是根据抽样方法的等比例性质以及互斥事件的概率来求解，属于基础题。