问题
解答题
已知函数y=x2（x＞0）的图象在点（ak，ak2）处的切线与x轴的交点的横坐标为ak+1（k∈N*），a1=1；数列{bn}满足：b1=2，且对任意p，q∈N*，都有bp+bq=bp+q。
（Ⅰ）求数列{an}、{bn}的通项公式；
（Ⅱ）求数列{an·bn}的前n项和Tn。
答案
解：（Ⅰ）
，∴
，
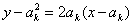令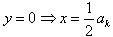
，即
，
∴
，
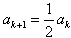令p=1，q=n，则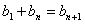
，
∴
。
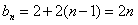（Ⅱ）
，
∴
， ①
②
①-②，得
，
∴
。
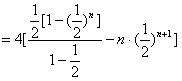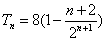