问题
解答题
已知数列{an}是等差数列,且a1=2,a1+a2+a3=12.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=an3n(x∈R).求数列{bn}前n项和的公式.
答案
解:(Ⅰ)设数列{an}公差为d,则 a1+a2+a3=3a1+3d=12,
又a1=2,d=2.
所以an=2n.
(Ⅱ)由bn=an3n=2n3n,得 Sn=2×3+4×32+…(2n﹣2)×3 n﹣1+2n×3n,①
3Sn=232+433+…+(2n﹣2)3n+2n3n+1.②
将①式减去②式,得﹣2Sn=﹣2(3+32+…3n)﹣2n3n+1
=3(3n﹣1)﹣2n3n+1.
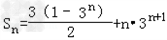 .
.
