问题
填空题
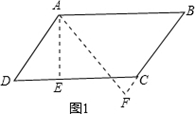
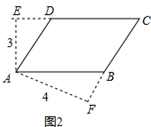
已知□ABCD的周长为28，自顶点A作AE⊥DC于点E，AF⊥BC于点F. 若AE=3，AF=4，则CE-CF= .
答案
14-7
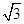或2-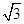
如图1：∵AE⊥DC，AF⊥BC，∴∠AED=∠AFB=90°，∵四边形ABCD是平行四边形，
∴∠ADC=∠CBA，AB=CD，AD=BC，∴△ADE∽△ABF，∴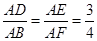
，∵AD+CD+BC+AB=28，
即AD+AB=14，∴AD=6，AB=8，∴DE=3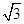，BF=4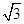，∴EC=CD-DE=8-3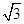，CF=BF-BC=4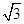-6，
∴CE-CF=（8-3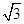）-（4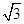-6）=14-7；
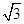如图2：∵AE⊥DC，AF⊥BC，∴∠AED=∠AFB=90°，∵四边形ABCD是平行四边形，
∴∠ADC=∠CBA，AB=CD，AD=BC，∴∠ADE=∠ABF，∴△ADE∽△ABF，∴，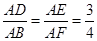
∵AD+CD+BC+AB=28，即AD+AB=14，∴AD=6，AB=8，∴DE=3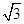，BF=4，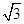
∴EC=CD+DE=8+3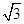，CF=BC+BF=6+4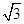，∴CE-CF=（8+3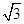）-（6+4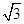）=2-．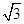
∴CE-CF=14-7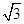或2-．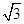
