问题
解答题
已知数列{an}的前n项和为Sn，且Sn=2an-2（n=1，2，3....），数列{bn}中，b1=1，点P（bn，bn+1）在直线x-y+2=0上。
（I）求数列{an}，{bn}的通项an和bn；
(II) 设cn=anbn，求数列{cn}的前n项和Tn，并求满足Tn<167的最大正整数n。
答案
解：（Ⅰ）∵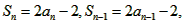
又
∴
∵
，
∴
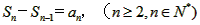
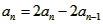
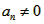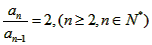，即数列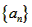
是等比数列，
∵
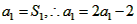，即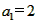
∴
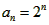
∵点P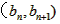
在直线x-y+2=0上，∴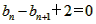
∴
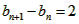，即数列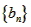
时等差数列，又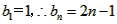
（Ⅱ）∵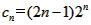
∴
，
∴
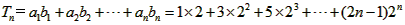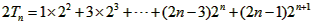
因此：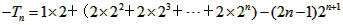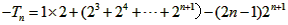
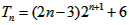
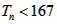即：
∴
∵
，即：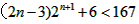
，
于是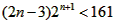
又由于当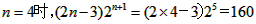
，
当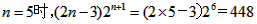
，
故满足条件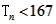
得最大正整数n为4。