问题
解答题
在某次测验中，有6位同学的平均成绩为75分．用xn表示编号为n(n＝1,2， ，6)的同学所得成绩，且前5位同学的成绩如下：
(2)从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间(68,75)中的概率． |
答案
(1) 7.(2) 0.4
题目分析：解 (1)∵这6位同学的平均成绩为75分，
∴
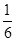(70＋76＋72＋70＋72＋x6)＝75，
解得x6＝90， 3分
这6位同学成绩的方差
s2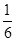＝×[(70－75)2＋(76－75)2＋(72－75)2＋(70－75)2＋(72－75)2＋(90－75)2]＝49，
∴标准差s＝7 6分
(2)从前5位同学中，随机地选出2位同学的成绩有：(70,76)，(70,72)，(70,70)，(70,72)，(76,72)，(76,70)，(76,72)，(72,70)，(72,72)，(70,72)，共10种， 9分
恰有1位同学成绩在区间(68,75)中的有：(70,76)，(76,72)，(76,70)，(76,72)，共4种，所求的概率为
＝0.4 11分
即恰有1位同学成绩在区间(68,75)中的概率为0.4 12分
点评：解决的关键是根据方差的定义得到求解，以及古典概型 概率公式来得到概率值，属于基础题。