（1）S_n＝2ⁿ⁺²＋n²＋3n－4（2）①a_n＝4n＋4，b_n＝2，②不存在

题目分析：（1）条件“a₁b₁＋a₂b₂＋a₃b₃＋···＋a_nb_n”实质为数列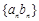前n项的和，所以按已知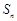求方法进行化简.∵a₁b₁＋a₂b₂＋a₃b₃＋···＋a_nb_n＝n·2ⁿ⁺³∴a₁b₁＋a₂b₂＋a₃b₃＋···＋a_n－1b_n－1＝(n－1)·2ⁿ⁺² (n≥2) 两式相减得：a_nb_n＝n·2ⁿ⁺³－(n－1)·2ⁿ⁺²＝(n＋1)·2ⁿ⁺² (n≥2) 而当n＝1时，a₁b₁＝2⁴适合上式，∴a_nb_n＝(n＋1)·2ⁿ⁺² (n∈N*)∵{b_n}是首项为4、公比为2的等比数列 ∴b_n＝2ⁿ⁺¹∴a_n＝2n＋2，∴{a_n＋b_n}的前n项和S_n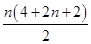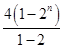＝＋＝2ⁿ⁺²＋n²＋3n－4（2）①由（1）有a_nb_n＝(n＋1)·2^n+2，设a_n＝kn＋b，则b_n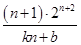＝∴b_n－1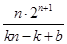＝ (n≥2) 设{b_n}的公比为q，则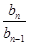＝＝q对任意的n≥2恒成立，即k(2－q)n²＋b(2－q)n＋2(b－k)＝0对任意的n≥2恒成立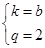，∴又∵a₁＝8，∴k＋b＝8∴k＝b＝4，∴a_n＝4n＋4，b_n＝2ⁿ②存在性问题，一般从假设存在出发，有解就存在，无解就不存在.本题从范围角度说明解不存在.

解：（1）∵a₁b₁＋a₂b₂＋a₃b₃＋···＋a_nb_n＝n·2ⁿ⁺³

∴a₁b₁＋a₂b₂＋a₃b₃＋···＋a_n－1b_n－1＝(n－1)·2ⁿ⁺² (n≥2)

两式相减得：a_nb_n＝n·2ⁿ⁺³－(n－1)·2ⁿ⁺²＝(n＋1)·2ⁿ⁺² (n≥2)

而当n＝1时，a₁b₁＝2⁴适合上式，∴a_nb_n＝(n＋1)·2ⁿ⁺² (n∈N*)

∵{b_n}是首项为4、公比为2的等比数列 ∴b_n＝2ⁿ⁺¹

∴a_n＝2n＋2，∴{a_n＋b_n}的前n项和S_n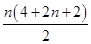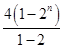＝＋＝2ⁿ⁺²＋n²＋3n－4

（2）①设a_n＝kn＋b，则b_n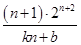＝，∴b_n－1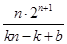＝ (n≥2)

设{b_n}的公比为q，则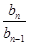＝＝q对任意的n≥2恒成立，

即k(2－q)n²＋b(2－q)n＋2(b－k)＝0对任意的n≥2恒成立，

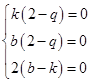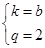∴ ∴ 又∵a₁＝8，∴k＋b＝8∴k＝b＝4，∴a_n＝4n＋4，b_n＝2ⁿ

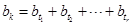②假设数列{b_n}中第k项可以表示为该数列中其它r项的和，即，从而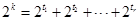，易知k≥t_r＋1 

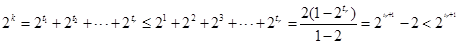
∴k＜t_r＋1，此与k≥t_r＋1矛盾，从而这样的项不存在．求,等差数列与等比数列基本性质