问题
问答题
某消费者具有效用函数U(X,Y)
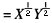 X和Y的单位价格均为4元,该消费者的收入为144元。试问: (1)为使消费者的效用最大化,消费者对X和Y的需求应该各为多少单位(要求写出最优化问题,然后求解。) (2)消费者的总效用是多少每单位货币的边际效用是多少 (3)若X的单位价格上升为9元,对两种商品的需求有何变化此时总效用为多少
X和Y的单位价格均为4元,该消费者的收入为144元。试问: (1)为使消费者的效用最大化,消费者对X和Y的需求应该各为多少单位(要求写出最优化问题,然后求解。) (2)消费者的总效用是多少每单位货币的边际效用是多少 (3)若X的单位价格上升为9元,对两种商品的需求有何变化此时总效用为多少
答案
参考答案:
解析:某消费者具有效用函数U(X,Y)
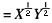 X和Y的单位价格均为4元,该消费者的收入为144元。试问: (1)为使消费者的效用最大化,消费者对X和Y的需求应该各为多少单位(要求写出最优化问题,然后求解。) (2)消费者的总效用是多少每单位货币的边际效用是多少 (3)若X的单位价格上升为9元,对两种商品的需求有何变化此时总效用为多少根据题意,预算方程为4X+4Y=144,那么144-4X-4Y=0 令U
X和Y的单位价格均为4元,该消费者的收入为144元。试问: (1)为使消费者的效用最大化,消费者对X和Y的需求应该各为多少单位(要求写出最优化问题,然后求解。) (2)消费者的总效用是多少每单位货币的边际效用是多少 (3)若X的单位价格上升为9元,对两种商品的需求有何变化此时总效用为多少根据题意,预算方程为4X+4Y=144,那么144-4X-4Y=0 令U
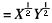 +λ(144-4X-4Y),U极大化的必要条件是所有一阶偏导数为零,即
+λ(144-4X-4Y),U极大化的必要条件是所有一阶偏导数为零,即
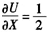 -4λ=0;
-4λ=0;
 -4λ=0;
-4λ=0;
 =144-4X-4Y=0 解下列方程组
=144-4X-4Y=0 解下列方程组
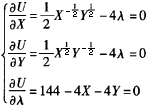 可得
可得
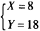 (2)总效用U
(2)总效用U
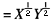 =
=
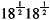 =18 每单位货币的边际效用是
=18 每单位货币的边际效用是
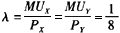 (3)若X的单位价格上升为9元,预算方程变为9X+4Y=144 解方程组
(3)若X的单位价格上升为9元,预算方程变为9X+4Y=144 解方程组
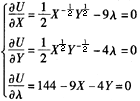 可得
可得
 总效用U=
总效用U=
 =12
=12
