问题
解答题
如果有穷数列a1,a2,a3,…,am(m为正整数)满足条件a1=am,a2=am-1,…,am=a1,即ai=am-i+1(i=1,2,…,m),我们称其为“对称数列”。
例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”。
(1)设{bn}是7项的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11,依次写出{bn}的每一项;
(2)设{cn}是49项的“对称数列”,其中c25,c26,…,c49是首项为1,公比为2的等比数列,求{cn}各项的和S;
(3)设{an}是100项的“对称数列”,其中d51,d52,…,d100是首项为2,公差为3的等差数列,求{dn}前n项的和Sn(n=1,2,…,100)。
答案
解:(1)设数列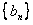 的公差为d,
的公差为d,
则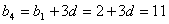 ,解得d=3,
,解得d=3,
∴数列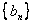 为2,5,8,11,8,5,2。
为2,5,8,11,8,5,2。
(2)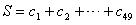
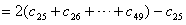
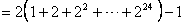
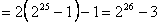 =67108861。
=67108861。
(3)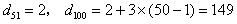 ,
,
由题意,得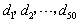 是首项为149,公差为-3的等差数列,
是首项为149,公差为-3的等差数列,
当n≤50时,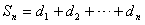
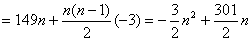 ;
;
当51≤n≤100时,
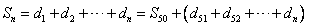
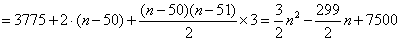 ,
,
综上所述,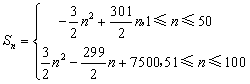 。
。
