解：（Ⅰ）n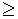2时，f（n）=S_n﹣S_n﹣1=2n+1．

n=1时，f（1）=S₁=3，适合上式，

∴f（n）=Sn﹣Sn﹣1=2n+1．（n∈N*）．

（Ⅱ）a₁=f（1）=3，a_n+1=2a_n+1，（n∈N*）．即a_n+1+1=2（a_n+1）．

∴数列{an+1}是首项为4，公比为2的等比数列．a_n+1=（a₁+1）2n+1=2n+1．

a_n=2n+1﹣1，（n∈N*）．

T_n=2²+2³+2⁴+…+2ⁿ⁺¹﹣n=2 ⁿ⁺²﹣4﹣n．