问题
解答题
已知:数列{an}的前n项和为Sn,且满足S2n-S2n-1=3n2an,a1=2,an≠0,n=2,3,4,…。
(1)设Cn=an+an+1,求C1,C2并判断数列{Cn}是否为等差数列,说明理由;
(2)求数列{(-1)n+1anan+1}的前2k+1项的和T2k+1。
答案
解:(1)当n≥2时,
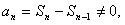
代入已知条件得:
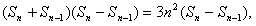
∴
由①得

∴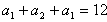
∵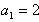
∴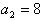
∴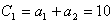
由①得
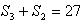
∴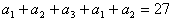
∴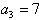
∴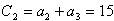
由①得
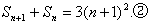
由②-①得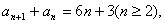
∴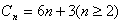
∵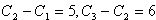
∴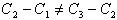
∴{cn}(n∈N*)不是等差数列。
(2)由(1)知

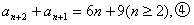
由④-③得
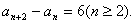
∴数列{a2n}是首项为a2=8,公差为6的等差数列,
数列{a2n-1}是首项为a3=7,公差为6的等差数列
∴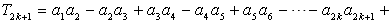
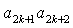
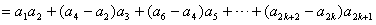
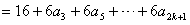
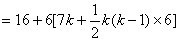
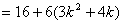
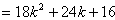 。
。

