问题
解答题
（1）已知a、b、c、d是成比例线段，其中a=3cm，b=2cm，c=6cm，求线段d的长．
（2）已知线段a、b、c，a=4cm，b=9cm，线段c是线段 a和b的比例中项．求线段c的长．
（3）已知y=y1+y2，y1与x成正比例，y2与x成反比例，且当x=1时，y=4，x=2时，y=5．
求：①y与x之间的函数关系式；②当x=4时，求y的值．
答案
（1）4cm （2）6cm （3）①y=2x+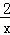
②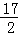
题目分析：（1）根据已知得到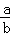
=
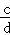，代入a、b、c的值即可求出；
（2）根据线段c是线段 a和b的比例中项，得到c2=ab，代入即可求出答案；
（3）①设y1=ax（a≠0）设y2=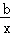
b≠0），根据已知得到y=ax+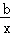，把当x=1，y=4和x=2，y=5代入即可求出a、b的值，即可得到答案；②把x=4代入①即可求出y的值．
解：（1）∵a、b、c、d是成比例线段，
∴=，
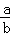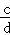∵a=3，b=2，c=6，
代入得：d=4，
答：线段d的长是4cm．
（2）解：∵线段c是线段 a和b的比例中项，
∴c2=ab，
∵a=4，b=9，代入得：c=6，
答：线段c的长是6cm．
（3）①解：∵y1与x成正比例，
设y1=ax，（a≠0），
∵y2与x成反比例，
设y2=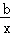（b≠0）
∴y=ax+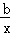
，
把x=1，y=4和x=2，y=5代入得：
，
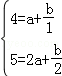解得：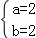
，
∴y=2x+，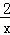
答：y与x之间的函数关系式是y=2x+．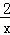
②解：由①知：y=2x+，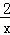
当x=4时，y=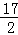
，
答：当x=4时，y的值是．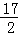
点评：本题主要考查了比例线段，比例的性质，用待定系数法求反比例函数、正比例函数的解析式等知识点，解此题的关键是能熟练地利用性质进行计算．
