问题
解答题
已知一个数列{an}的各项是1或2.首项为1,且在第k个1和第k+1个1之间有f(k)个2,记数列的前n项的和为Sn.
(1)若f(k)=2k﹣1,求S100;
(2)若f(k)=2k﹣1,求S2011.
答案
解:(1)若f(k)=2k﹣1,则数列为1,2,1,2,2,1,2,2,2,1…
记第k个1与其后面的k个2组成第k组,其组内元素个数记为bk,则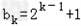
又当k=6时,b1+b2+…+b6=2+3+5+9+17+33=69<100
但当k=6时,b1+b2+…+b7=2+3+5+9+17+33+65=134>100
所以前100项中由前6组以及第7组的部分元素构成,
故有7个1和93个2,从而S100=7+93×2=193
(2)若f(k)=2k﹣1,则数列为1,2,1,2,2,2,1,2,2,2,2,2,1…
记第k个1与其后面的k个2组成第k组,其组内元素个数记为bk,则bk=2k
令b1+b2+…+bn=2+4+…+2n=n(n+1)<2011,
而44×45=1980<2011,45×46=2070>2011
故n=44,即前2011项中有45个以及1966个2,所以S2011=45+1966×2=3977
