问题
填空题
在Rt△ABC中,∠C=90°,CD⊥AB于点D,若AD=9,BD=4,则AC= .
答案
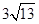 .
.
题目分析:根据题意画出图形,先根据相似三角形的判定定理得出△ACD∽△CBD,再由相似三角形的对应边成比例求出CD的长,根据勾股定理即可得出AC的长
如图所示:
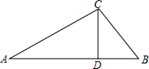
∵Rt△ABC中∠C=90°,CD⊥AB,
∴∠A+∠B=90°,∠A+∠ACD=90°,∠B+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴CD:AD="BD:CD" ,即CD2=AD•BD=9×4=36,解得CD=6,
在Rt△ACD中,
∵AD=9,CD=4,
∴AC=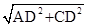 =
=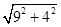 =5.
=5.
故答案为:5.