问题
解答题
已知数列 {an}的前n项和Sn=2n2-3n
(1)证明数列{an}是等差数列.
(2)若bn=an·2n,求数列{bn}的前n项和Tn.
答案
解:(1)a1=S1=-1
当n≥2时,an=Sn-Sn﹣1=2n2-3n-2(n-1)2+3(n-1)=4n-5
又a1适合上式 an=4n﹣5(n∈N*)
当n≥2时,an﹣an﹣1=4n-5-4(n-1)+5=4
{an}是等差数列且d=4,a1=-1
(2)bn=(4n﹣5)2n(差比数列求和)
∴Sn=﹣21+3·22+…(4n﹣5)·2n①
2Sn=﹣22+…+(4n﹣9)·2n+(4n﹣5)·2n+1②
①﹣②得﹣Sn=﹣21+4·22+…+4·2n﹣(4n﹣5)·2n+1
=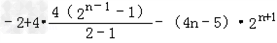
=﹣18﹣(4n﹣9)·2n+1
∴Sn=18+(4n﹣9)·2n+1