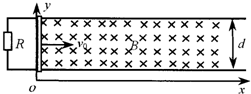
如图所示,两根相距为d足够长的平行光滑金属导轨位于水平的xoy平面内,导轨与x轴平行,一端接有阻值为R的电阻.在x>0的一侧存在竖直向下的匀强磁场,一电阻为r的金属直杆与金属导轨垂直放置,并可在导轨上滑动.开始时,金属直杆位于x=0处,现给金属杆一大小为v0、方向沿x轴正方向的初速度.在运动过程中有一大小可调节的平行于x轴的外力F作用在金属杆上,使金属杆保持大小为a、方向沿x轴负方向的恒定加速度运动.金属轨道电阻可忽略不计.
求:
(1)金属杆减速过程中到达x=x0处位置时金属杆的感应电动势E;
(2)回路中感应电流方向发生改变时,金属杆在轨道上的位置;
(3)若金属杆质量为m,请推导出外力F随金属杆在x轴上的位置(x)变化关系的表达式.
(1)设金属杆到达x0处时,其速度为v1,由运动学公式
-v 21
=-2ax0 v 20
解得:v1=
-2ax0v 20
故金属杆的感应电动势为 E=Bdv1=Bd
-2ax0v 20
(2)当金属杆的速度减小到零时,回路中感应电流方向改变,设此时金属杆的位置为xm
由运动学公式得
=2axmv 20
解得 xm=v 20 2a
(3)在金属杆沿x轴正方向运动的过程中,设金属杆到达x处时,速度大小为v,则
v=
-2axv 20
金属杆的感应电动势为E=Bdv
回路中的感应电流为I=E R+r
金属杆受到的安培力为FA=BId,方向为x轴负方向
设x负方向为正方向,由牛顿第二定律得 F+FA=ma
外力F随金属杆的位置x变化的关系为:F=ma-B2d2
-2axv 20 R+r
在金属杆沿x轴负方向运动的过程中,设金属杆到达x处时,速度大小为v,根据匀变速直线运动的对称性可知,v=
-2axv 20
同理,此金属杆的感应电动势为E=Bdv,
金属杆所受的安培力为:FA=BId=
,方向为x轴正方向B2d2
-2axv 20 R+r
设负x方向为正方向,由牛顿第二定律F-FA=ma
外力F随金属杆位置x变化的关系为:F=ma+B2d2
-2axv 20 R+r
答:
(1)金属杆减速过程中到达x=x0处位置时金属杆的感应电动势E为Bd
;
-2ax0v 20
(2)回路中感应电流方向发生改变时,金属杆在轨道上的位置为
;v 20 2a
(3)若金属杆质量为m,外力F随金属杆在x轴上的位置(x)变化关系的表达式为:
在金属杆沿x轴正方向运动的过程中,F=ma-
;在金属杆沿x轴负方向运动的过程中,F=ma+B2d2
-2axv 20 R+r
.B2d2
-2axv 20 R+r
