问题
解答题
已知{an}是等差数列，其前n项和为Sn，{bn}是等比数列，且a1=b1=2，a4+b4=27，S4-b4=10。
（1）求数列{an}与{bn}的通项公式；
（2）记Tn=anb1+an-1b2+…+a1bn，n∈N*，证明：Tn-8=an-1bn+1（n∈N*，n≥2）。
答案
解：（1）设等差数列的公差为d，等比数列的首项为q，
由a1=b1=2，得a4=2+3d，b4=2q3，
S4=8+6d，由a4+b4=27，S4-b4=10，
得方程组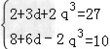
，解得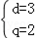
，
所以：an=3n-1，bn=2n。
（2）证明：由第一问得：Tn=anb1+an-1b2+…+a1bn=2×2+5×22+8×23+…+（3n-1）×2n； ①；
2Tn=2×22+5×23+…+（3n-4）×2n+（3n-1）×2n+1，②
由①-②得，-Tn=2×2+3×22+3×23+…+3×2n-（3n-1）×2n+1
= 
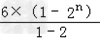-（3n-1）×2n+1-2
=-（3n-4）×2n+1-8
即Tn-8=（3n-4）×2n+1
而当n≥2时，an-1bn+1=（3n-4）×2n+1
∴Tn-8=an-1bn+1（n∈N*，n≥2）。