问题
填空题
在△ABC中,AB=24,AC=18,D是AC上一点且AD=12,在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE= .
答案
9或16.
题目分析:根据相似三角形的判断,要使得△ADE与△ABC相似,已经满足∠BAC=∠DAE,因此只要两边对应成比例即可,由于本题中三角形相似,对应点没有确定,因此分两种情况,画出图形,然后根据相似三角形对应边成比例,就出AE的长.
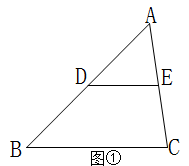
第一种情况:当△ABC∽△ADE时,如图①;
∵△ABC∽△ADE,
∴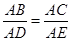 ,
,
∵AB=24,AC=18,AD=12,
∴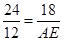 ,
,
∴AE=9.
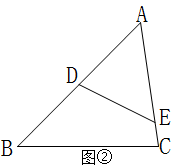
第二种情况:当△ABC∽△AED,如图②;
∵△ABC∽△AED,
∴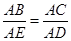 ,
,
∵AB=24,AC=18,AD=12,
∴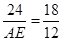 ,
,
∴AE=16.
故填9或16.