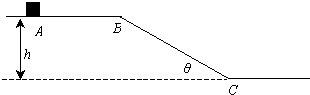
如图所示,一高度为h=0.8m粗糙的水平面在B点处与一倾角为θ=30°光滑的斜面BC连接,一小滑块从水平面上的A点以v0=3m/s的速度在粗糙的水平面上向右运动.运动到B点时小滑块恰能沿光滑斜面下滑.已知AB间的距离s=5m,求:
(1)小滑块与水平面间的动摩擦因数;
(2)小滑块从A点运动到地面所需的时间;
(3)若小滑块从水平面上的A点以v1=5m/s的速度在粗糙的水平面上向右运动,运动到B点时小滑块将做什么运动?并求出小滑块从A点运动到地面所需的时间.(取g=10m/s2).
(1)小滑块运动到B点时速度恰为零,设小滑块在水平面上运动的加速度大小为a,
据牛顿第二定律可得 μmg=ma ①
由运动学公式得-v02=-2as②
解得 μ=0.09③
故小滑块与水平面间的动摩擦因数为0.09.
(2)小滑块运动到B点 t1=
=3.3s ④v0 μg
在斜面上运动的加速度a=gsinθ,
运动的时间 t2=
=0.8s⑤2h gsin2θ
小滑块从A点运动到地面所需的时间为 t=t1+t2=4.1s ⑥
故小滑块从A点运动到地面所需的时间为4.1s.
(3)若小滑块从水平面上的A点以v1=5m/s的速度在粗糙的水平面上向右运动,运动到B点时的速度为,
由vB2-v12=-2as得vB=
=4m/s v12-2as
小滑块将做平抛运动.
假设小滑块不会落到斜面上,则经过t3=
=0.4s,由于水平运动的位移x=vBt3=1.67m>2h g
=1.36mh tan30°
所以假设正确.
小滑块从A点运动到地面所需的时间为t=t3+
=1.5s ⑨2s v1+vB
故小滑块从A点运动到地面所需的时间为1.5s.
