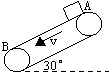
如图所示,A、B两轮间距为L=3.25m,套有传送带,传送带与水平方向成α=30°角,传送带始终以2m/s的速率运动.将一物体轻放在A轮处的传送带上,物体与传送带间的滑动摩擦系数为μ=
/5,g取10m/s2.则:3
(1)物体从A运动到B所需的时间为多少?
(2)若物体与传送带间的滑动摩擦系数为μ=
,物体从A运动到B所需的时间为多少?3 2
(1)根据牛顿第二定律得:mgsin30°+μmgcos30°=ma1
初始加速度a1=g(sin30°+μcos30°)=8m/s2
第一段匀加速直线运动的位移s1=
=0.25m 时间t1=v2 2a
=0.25sv a
同理第二段加速度a2=g(sin30°-μcos30°)=2m/s2
第二段位移s2=L-s1=3m s2=vt2+
a21 2
t2=1st 22
故t=t1+t2=1.25s
(2)根据牛顿第二定律得:mgsin30°+μmgcos30°=ma
初始加速度a=g(sin30°+μcos30°)=12.5m/s2
第一段匀加速直线运动的位移s1=
=0.16m 时间t1=v2 2a
=0.16s v a
当物体与传送带速度相同的瞬间,由于mgsin30°<μmgcos30° 物体与传送带相对静止,一起匀速运动
则第二段位移s2=L-s1=3.09m t2=
=1.545s s2 v
故t=t1+t2=1.705s
答:(1)物体从A运动到B所需的时间为1.25s.
(2)若物体与传送带间的滑动摩擦系数为μ=
,物体从A运动到B所需的时间为1.705s.3 2
