问题
填空题
关于函数f(x)=lg
①其图象关于y轴对称; ②当x>0时,f(x)是增函数;当x<0时,f(x)是减函数; ③f(x)的最小值是lg2; ④f(x)在区间(-1,0)、(2,+∞)上是增函数; ⑤f(x)无最大值,也无最小值 其中所有正确结论的序号是______. |
答案
①定义域为R,又满足f(-x)=f(x),所以函数y=f(x)的图象关于y轴对称,正确.
②令t=x+
(x>0),在(0,1]上是减函数,在[1,+∞)上是增函数,不正确.1 x
③t=x+
≥2,又是偶函数,所以函数f(x)的最小值是lg2,正确.1 x
④当-1<x<0或x>1时函数t=x+
是增函数,根据复合函数知,f(x)是增函数,正确.1 x
⑤由③知,不正确.
故答案为:①③④

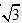 A
A /2
/2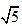 /2A
/2A