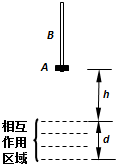
在地面上方足够高的地方,存在一个高度d=0.3m的“相互作用区域”(如图中划有虚线的部分).一个小圆环A套在一根均匀直杆B上,A和B的质量均为m,若它们之间发生相对滑动时,会产生f=0.5mg的摩擦力.开始时A处于B的最下端,B竖直放置,A距“相互作用区域”的高度h=0.2m.让A和B一起从静止开始下落,只要A处于“相互作用区域”就会受到竖直向上的恒力F作用(F=2mg),而“相互作用区域”对处于其中的杆B不产生作用力.设杆B在下落过程中始终保持竖直,且杆的长度能够保证圆环A与杆不会分离.不计空气阻力,取g=10m/s2.求:
(1)杆B刚进人“相互作用区域”时的速度.
(2)圆环A通过“相互作用区域”所用的时间.
(3)A刚离开“相互作用区域”时,圆环A和直杆B的速度.
(4)假如直杆B着地时,A和B的速度刚好达到相同,这一速度是多少?
(1)设A和B一起静止下落至“相互作用区域”的速度为v1,根据动能定理有
2mgh=
•2m1 2
,v 21
代入数据解得:v1=2.0m/s
(2)过程1:A在“相互作用区域”运动时,取方向向下为正方向,此过程中A受到竖直向下的重力mg、滑动摩擦力f和竖直向上的恒力F作用.
设加速度aA1、末速度为vA、运动时间为t1,根据牛顿第二定律有:
aA1=
=-mg+f-F m
g1 2
根据运动学公式有:vA=v0+aA1t1,d=
-v 2A v 20 2 a A1
代入数据解出:t1=0.2s t2=0.6s(不符题意,舍去)
(3)A离开“相互作用区域”时的速度为 vA=v0+aA1t1=1m/s
B受到竖直向下的重力mg和竖直向上的滑动摩擦力f的作用
同理有:aB1=
=mg-f m
g1 2
vB=v0+aB1t1 代入数据:vB=3m/s
(4)过程2:A离开“相到作用区域”后,因为vA<vB,所以A受到竖直向下的重力mg和滑动摩擦力f的作用,B受到竖直向下重力mg和竖直向上的滑动摩擦力f的作用.
设加速度分别为aA2、aB2,共同速度为v,运动时间为t2
则有:aA2=
=mg+f m
g,aB2=3 2
=mg-f m
g1 2
又v=vA+aA2t2,v=vB+aB2t2
由上述四式代入数据解得:v=4m/s
答:
(1)杆B刚进人“相互作用区域”时的速度是2m/s.
(2)圆环A通过“相互作用区域”所用的时间是0.2m/s.
(3)A刚离开“相互作用区域”时,圆环A和直杆B的速度分别是1m/s和3m/s.
(4)假如直杆B着地时,A和B的速度刚好达到相同,这一速度是4m/s.
