参考答案：

各方案的总成本C均是产量Q的函数，即

C_A＝1 350+0.18Q

C_B＝950+0.2Q

C_C＝680+0.23Q

因此首先以Q为变量，做出三个方案的总成本线

(C线)，如图8-3所示。

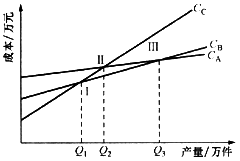
从图8-3中可见，三条C线分别两两相交于Ⅰ、Ⅱ、Ⅲ三点，则这三点就分别是相应的两个方案的盈亏

图8-3 A、B、C方案总成本线平衡点。其对应的产量就是盈亏平衡产量。例如，C_B和C_C相交于I点，则Ⅰ点就是方案B和方案C的盈亏平衡点，Q₁就是方案B和方案C的盈亏平衡产量。也就是说，当产量水平为Q₁时，从成本分析的角度，方案B和方案C是完全相同的两个方案。

下面根据盈亏平衡点的定义来分别计算Q₁、Q₂和Q₃。

当产量水平为Q₁时，C_B＝C_C，即

950+0.2Q₁＝680+0.23Q₁

可解得：Q₁＝0.9万件

当产量水平为Q₂时，C_A＝C_C，即

1 350+0.18Q₂＝680+0.23Q₂

可解得：Q₂＝1.34万件

当产量水平为Q₃时，C_A＝C_B，即

1 350+0.18Q₃＝950+0.2Q₃

可解得：Q₃＝2万件

由于各生产线的生产能力是相同的，因此确定各方案适用的生产规模也就是比较各种生产规模下各个方案的成本情况。由上面的计算结果可知，当产量水平低于0.9万件时，以方案C为最经济，当产量水平在0.9～2万件时，以方案B为最佳，而当产量水平高于2万件时，又以方案A最为合理。