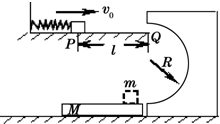
如图所示,水平轨道上,轻弹簧左端固定,自然状态时右端位于P点.现用一质量m=0.1kg的小物块(视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=18m/s,经过水平轨道右端Q点后恰好沿半圆轨道的切线进入竖直固定的圆轨道,最后滑上质量M=0.9kg的长木板(木板足够长,物块滑上去不会从木板上掉下来).已知PQ间的距离l=1m,竖直半圆轨道光滑且半径R=1m,物块与水平轨道间的动摩擦因数µ1=0.15,与木板间的动摩擦因数µ2=0.2,木板与水平地面间的动摩擦因数µ3=0.01,取g=10m/s2.
(1)判断物块经过Q点后能否沿圆周轨道运动;
(2)求木板滑行的最大距离x.
(1)物块在PQ上运动的加速度
a1=-µ1g=-1.5m/s2
进入圆周轨道时的速度为v
v2-v02=2a1l
得v2=v02+2a1l=321 m2/s2
设物块刚离开Q点时,圆轨道对物块的压力为FN,
根据牛顿定律,有FN+mg=mv2 R
FN=m
-mg=31.1N>0v2 R
故物块能沿圆周轨道运动
(2)物块滑上木板时的速度为v1
根据机械能守恒有
mv2+mg•2R=1 2
mv121 2
得v1=19m/s
物块滑上木板时的加速度为a2
根据牛顿第二定律有
a2=-µ2g=-2m/s2
木板的加速度位a3
µ2mg-µ3(m+M)g=Ma3
a3=
=μ2mg-μ3(M+m)g M
m/s21 9
设物块滑上木板经过时间t二者共速,
v1+a2t=a3t 得t=9s
这时木板的位移s1=
a3t2=4.5m1 2
它们的共同速度v2=a3t=1m/s
物块和木板一起减速的加速度a4=-µ3g=-0.1m/s2
它们减速运动的位移s2=
=5m-v22 2a4
x=s1+s2=9.5m
答:(1)物块能沿圆周轨道运动;
(2)木板滑行的最大距离x为9.5m.
