问题
填空题
函数:f(x)=log2
|
答案
因为函数f(x)=log2
,所以该函数的定义域满足:1 2-x2
⇒-2-x2≠0
>01 2-x2
< x<2
;2
令t=
x∈(-1 2-x2
,2
),2-x2∈(0,2],2
利用不等式的性质得:t≥
,有求函数值域的换元法得到:y=f(t)=log2t,t∈[1 2
,+∞),1 2
利用此对数函数在定义域内为单调递增函数,
所以y=f(x)的值域就等于y=f(t)的值域为[-1,+∞)
故答案为:(-
,2
) ;[-1,+∞)2

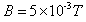 ,方向垂直纸面向里,现有带正电的粒子流沿两板中OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,重力忽略不计,在每个粒子通过电场区域的极短时间内,电场可视作是恒定不变的。
,方向垂直纸面向里,现有带正电的粒子流沿两板中OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,重力忽略不计,在每个粒子通过电场区域的极短时间内,电场可视作是恒定不变的。