问题
解答题
2012年3月2日，国家环保部发布了新修订的《环境空气质量标准》．其中规定：居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称可入肺颗粒物)年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米．某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据，数据统计如下：
(2)求该样本的平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境是否需要改进？说明理由； (3)将频率视为概率，对于去年的某2天，记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X，求X的分布列及数学期望E(X)． |
答案
（1）22.5，37.5（2）需要改进（3）1.8(天)
X的分布列为
| X | 0 | 1 | 2 |
| P |  |  |  |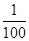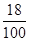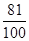
(1)众数为22.5微克/立方米，中位数为37.5微克/立方米．
(2)去年该居民区PM2.5年平均浓度为7.5×0.1＋22.5×0.3＋37.5×0.2＋52.5×0.2＋67.5×0.1＋82.5×0.1＝40.5(微克/立方米)．因为40.5>35，所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准，故该居民区的环境需要改进．
(3)记事件A表示“一天中PM 2.5的24小时平均浓度符合环境空气质量标准”，则P(A)＝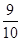
.随机变量X的可能取值为0，1，2，且X～B
.
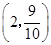所以P(X＝k)＝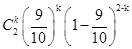
(k＝0，1，2)，
所以X的分布列为
| X | 0 | 1 | 2 |
| P | | | |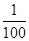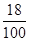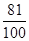
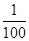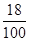＋1×＋2×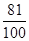＝1.8(天)或E(X)＝np＝2×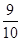＝1.8(天)．