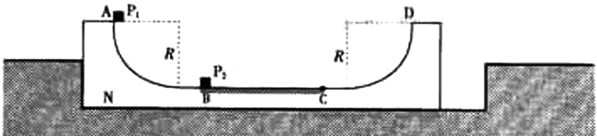
如图所示,固定的凹槽水平表面光滑,其内放置U形滑板N,滑板两端为半径R=0.45m的1/4圆弧面.A和D分别是圆弧的端点,BC段表面粗糙,其余段表面光滑.小滑块P1和P2的质量均为m.滑板的质量M=4m,P1和P2与BC面的动摩擦因数分别为μ1=0.10和μ2=0.40,最大静摩擦力近似等于滑动摩擦力.开始时滑板紧靠槽的左端,P2静止在粗糙面的B点,P1以v0=4.0m/s的初速度从A点沿弧面自由滑下,与P2发生弹性碰撞后,P1处在粗糙面B点上.当P2滑到C点时,滑板恰好与槽的右端碰撞并与槽牢固粘连,P2继续运动,到达D点时速度为零.P1与P2视为质点,取g=10m/s2.问:
(1)P2在BC段向右滑动时,滑板的加速度为多大?
(2)BC长度为多少?N、P1和P2最终静止后,P1与P2间的距离为多少?
(1)P1滑到最低点速度为v1,由机械能守恒定律有:
m1 2
+mgR=v 20
m1 2
解得:v1=5m/sv 21
P1、P2碰撞,满足动量守恒,机械能守恒定律,设碰后速度分别为v′1、v′2
则由动量守恒和机械能守恒可得:
mv1=mv′1+mv′2
m1 2
=v 21
mv1 2
+′ 21
mv1 2 ′ 22
解得:v′1=0、v′2=5m/s
P2向右滑动时,假设P1保持不动,对P2有:f2=μ2mg=4m(向左)
对P1、M有:f=(m+M)a2
a2=
=f m+M
=0.8m/s24m 5m
此时对P1有:f1=ma=0.80m<fm=1.0m,所以假设成立.
故滑块的加速度为0.8m/s2;
(2)P2滑到C点速度为v2′,由mgR=
mv1 2 ′ 22
得v′2=3m/s
P1、P2碰撞到P2滑到C点时,设P1、M速度为v,对动量守恒定律:mv2=(m+M)v+mv′2
解得:v=0.40m/s
对P1、P2、M为系统:f2L=
m1 2
-v 22
mv′22+1 2
(m+M)v21 2
代入数值得:L=1.9m
滑板碰后,P1向右滑行距离:S1=
=0.08mv2 2a1
P2向左滑行距离:S2=
=1.125mv ′ 22 2a2
所以P1、P2静止后距离:△S=L-S1-S2=0.695m
故最后两物体相距0.695m.
