问题
解答题
一台机器使用时间较长，但还可以使用.它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有 缺点零件的多少，随机器运转的速度而变化，下表为抽样试验结果：
（2）如果y与x有线性相关关系，求回归直线方程； （3）若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么，机器的运转速度应控制在什么范围内？ |
答案
（1）y与x有很强的线性相关关系（2）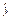
="0.728" 6x-0.857 1（3）机器的转速应控制在14.901 3转/秒以下
（1）
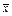=12.5,
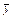=8.25,
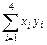=438，4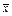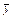=412.5，
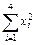=660，
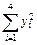=291，
所以r=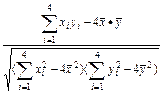
=
=
≈
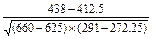
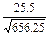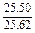≈0.995 4.
因为r＞r0.05,所以y与x有很强的线性相关关系.
（2）
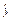="0.728" 6x-0.857 1.
（3）要使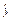≤10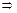
0.728 6x-0.857 1≤10,
所以x≤14.901 3.所以机器的转速应控制在14.901 3转/秒以下.